Eigenvectors animated gif

We have already seen how to make an animation using pylab. In this post we will use a trick proposed here by Alemi to make another animation. The animation we are going to see shows the eigenvectors of a matrix A 2-by-2 and the result of the linear application A*v when v is a vector that lies on the unit circle. Each frame of the animation is generated by the following script:

from pylab import arrow,axis,clf,savefig,plot
from numpy import array,pi,cos,sin,dot
from numpy.linalg import eig

theta = pi/9
R = array([ [cos(theta), -sin(theta)],  # rotation matrix
            [sin(theta), cos(theta)] ])
v = array([0,1]) # y axis versor

A = array([ [3, -1],  # transformation matrix
            [0,  2] ])
eival,eivec = eig(A) # eigen values and eigenvectors

for i in range(18):
 v = dot(R,v) # theta radiants rotation of v
 y = dot(A,v) # transformation
 # current original vector
 arrow(0,0,v[0],v[1], width=0.01, color='b')
 # current resulting vector
 arrow(0,0,y[0],y[1], width=0.01, color='g') 
 # ellipse axis
 arrow(0,0,eival[0]*eivec[0,0],eival[0]*eivec[1,0], width=0.01, color='y') # major
 arrow(0,0,eival[1]*eivec[0,1],eival[1]*eivec[1,1], width=0.01, color='y') # minor
 # 1st eigenvector
 arrow(0,0,eivec[0,0],eivec[1,0], width=0.01, color='r')
 # 2nd eigenvector
 arrow(0,0,eivec[0,1],eivec[1,1], width=0.01, color='r')
 axis([-3.5,3.5,-3.5,3.5])
 savefig('rotation/'+'0'+str(i+1)+'.png') # save the frame
 clf() # figure clear

And the animated gif is created using the command convert in the directory where the frames have been saved:

$ cd rotation
$ convert *.png -delay 50 -layers Optimize anim.gif

The command is provided by the ImageMagick suite available under linux. Click on the following image to see the animation.

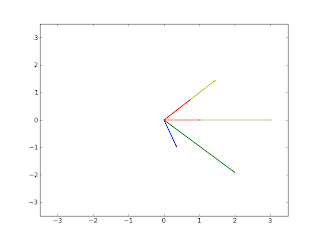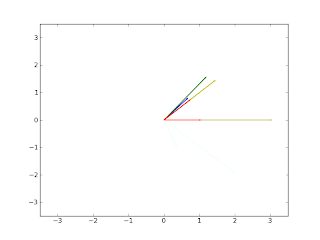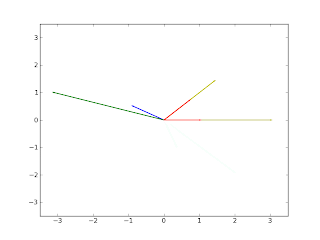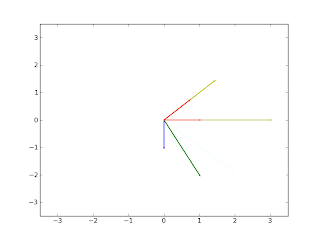
The vector v is represented by the blue arrow, A*v is the green arrow, the eigenvectors are the red arrows, and the yellow arrows are the eigenvectors multiplied by the their respective eigenvalues.