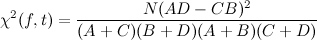Where f is a feature (a term in this case), t is a target variable that we, usually, want to predict, A is the number of times that f and t cooccur, B is the number of times that f occurs without t, C is the number of times that t occurs without f, D is the number of times neither t or f occur and N is the number of observations.
Let's see how χ2 can be used through a simple example. We load some posts from 4 different newsgroups categories using the sklearn interface:
from sklearn.datasets import fetch_20newsgroups
# newsgroups categories
categories = ['alt.atheism','talk.religion.misc',
'comp.graphics','sci.space']
posts = fetch_20newsgroups(subset='train', categories=categories,
shuffle=True, random_state=42,
remove=('headers','footers','quotes'))
From the posts loaded, we build a linear model using all the terms in the document collection but the stop words:
from sklearn.feature_extraction.text import CountVectorizer vectorizer = CountVectorizer(lowercase=True,stop_words='english') X = vectorizer.fit_transform(posts.data)Now, X is a document-term matrix where the element Xi,j is the frequency of the term j in the document i. Then, the features are given by the columns of X and we want to compute χ2 between the categories of interest and each feature in order to figure out what are the most relevant terms. This can be done as follows
from sklearn.feature_selection import chi2 # compute chi2 for each feature chi2score = chi2(X,posts.target)[0]To have a visual insight, we can plot a bar chart where each bar shows the χ2 value computed above:
from pylab import barh,plot,yticks,show,grid,xlabel,figure
figure(figsize=(6,6))
wscores = zip(vectorizer.get_feature_names(),chi2score)
wchi2 = sorted(wscores,key=lambda x:x[1])
topchi2 = zip(*wchi2[-25:])
x = range(len(topchi2[1]))
labels = topchi2[0]
barh(x,topchi2[1],align='center',alpha=.2,color='g')
plot(topchi2[1],x,'-o',markersize=2,alpha=.8,color='g')
yticks(x,labels)
xlabel('$\chi^2$')
show()
We can observe that the terms with a high χ2 can be considered relevant for the newsgroup categories we are analyzing. For example, the terms space, nasa and launch can be considered relevant for the group sci.space. The terms god, jesus and atheism can be considered relevant for the groups alt.atheism and talk.religion.misc. And, the terms image, graphics and jpeg can be considered relevant in the category comp.graphics.