Ridgeline plots in pure matplotlib

A Ridgeline plot (also called Joyplot) allows us to compare several statistical distributions. In this plot each distribution is shown with a density plot, and all the distributions are aligned to the same horizontal axis and, sometimes, presented with a slight overlap.

There are many options to make a Ridgeline plot in Python (joypy being one of them) but I decided to make my own function using matplotlib to have full flexibility and minimal dependencies:

from scipy.stats.kde import gaussian_kde
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt

def ridgeline(data, overlap=0, fill=True, labels=None, n_points=150):
    """
    Creates a standard ridgeline plot.

    data, list of lists.
    overlap, overlap between distributions. 1 max overlap, 0 no overlap.
    fill, matplotlib color to fill the distributions.
    n_points, number of points to evaluate each distribution function.
    labels, values to place on the y axis to describe the distributions.
    """
    if overlap > 1 or overlap < 0:
        raise ValueError('overlap must be in [0 1]')
    xx = np.linspace(np.min(np.concatenate(data)),
                     np.max(np.concatenate(data)), n_points)
    curves = []
    ys = []
    for i, d in enumerate(data):
        pdf = gaussian_kde(d)
        y = i*(1.0-overlap)
        ys.append(y)
        curve = pdf(xx)
        if fill:
            plt.fill_between(xx, np.ones(n_points)*y, 
                             curve+y, zorder=len(data)-i+1, color=fill)
        plt.plot(xx, curve+y, c='k', zorder=len(data)-i+1)
    if labels:
        plt.yticks(ys, labels)

The function takes in input a list of datasets where each dataset contains the values to derive a single distribution. Each distribution is estimated using Kernel Density Estimation, just as we've seen previously, and plotted increasing the y value.

Let's generate data from few normal distributions with different means and have a look at the output of the function:

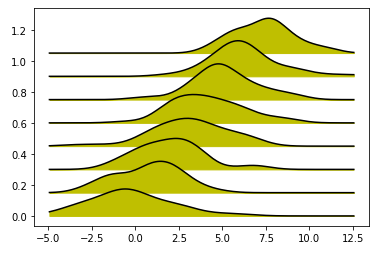
data = [norm.rvs(loc=i, scale=2, size=50) for i in range(8)]
ridgeline(data, overlap=.85, fill='y')

Not too bad, we can clearly see that each distribution has a different mean. Let's apply the function on real world data:

import pandas as pd
data_url = 'ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_weekly_mlo.txt'
co2_data = pd.read_csv(data_url, sep='\s+', comment='#', na_values=-999.99,
                       names=['year', 'month', 'day', 'decimal', 'ppm', 
                       'days', '1_yr_ago',  '10_yr_ago', 'since_1800'])
co2_data = co2_data[co2_data.year >= 2000]
co2_data = co2_data[co2_data.year != 2020]

plt.figure(figsize=(8, 10))
grouped = [(y, g.ppm.dropna().values) for y, g in co2_data.groupby('year')]
years, data = zip(*grouped)
ridgeline(data, labels=years, overlap=.85, fill='tomato')
plt.title('Distribution of CO2 levels per year since 2000',
          loc='left', fontsize=18, color='gray')
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.xlabel('ppm')
plt.xlim((co2_data.ppm.min(), co2_data.ppm.max()))
plt.ylim((0, 3.1))
plt.grid(zorder=0)
plt.show()

In the snippet above we downloaded the measurements of the concentration of CO2 in the atmosphere, the same data was also used here, and grouped the values by year. Then, we generated a Ridgeline plot that shows the distribution of CO2 levels each year since 2000. We easily note that the average concentration went from 370ppm to 420pmm gradually increasing over the 19 years abserved. We also note that the span of each distribution is approximatively 10ppm.