from pylab import arrow,axis,clf,savefig,plot
from numpy import array,pi,cos,sin,dot
from numpy.linalg import eig
theta = pi/9
R = array([ [cos(theta), -sin(theta)], # rotation matrix
[sin(theta), cos(theta)] ])
v = array([0,1]) # y axis versor
A = array([ [3, -1], # transformation matrix
[0, 2] ])
eival,eivec = eig(A) # eigen values and eigenvectors
for i in range(18):
v = dot(R,v) # theta radiants rotation of v
y = dot(A,v) # transformation
# current original vector
arrow(0,0,v[0],v[1], width=0.01, color='b')
# current resulting vector
arrow(0,0,y[0],y[1], width=0.01, color='g')
# ellipse axis
arrow(0,0,eival[0]*eivec[0,0],eival[0]*eivec[1,0], width=0.01, color='y') # major
arrow(0,0,eival[1]*eivec[0,1],eival[1]*eivec[1,1], width=0.01, color='y') # minor
# 1st eigenvector
arrow(0,0,eivec[0,0],eivec[1,0], width=0.01, color='r')
# 2nd eigenvector
arrow(0,0,eivec[0,1],eivec[1,1], width=0.01, color='r')
axis([-3.5,3.5,-3.5,3.5])
savefig('rotation/'+'0'+str(i+1)+'.png') # save the frame
clf() # figure clear
And the animated gif is created using the command convert in the directory where the frames have been saved: $ cd rotation $ convert *.png -delay 50 -layers Optimize anim.gifThe command is provided by the ImageMagick suite available under linux. Click on the following image to see the animation.
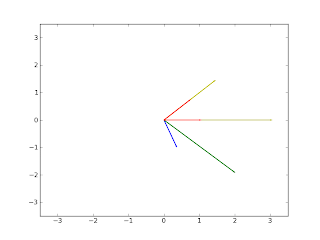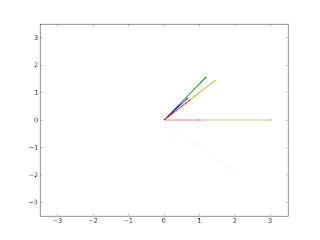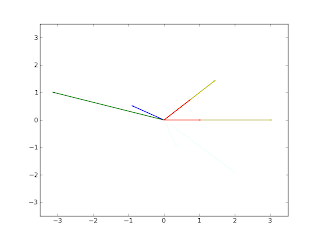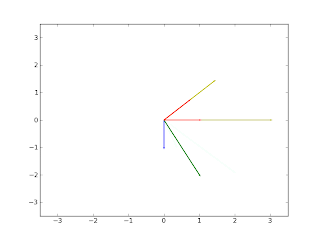
The vector v is represented by the blue arrow, A*v is the green arrow, the eigenvectors are the red arrows, and the yellow arrows are the eigenvectors multiplied by the their respective eigenvalues.

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.